Pada pembahasan sebelumnya, kalian telah mengetahui jika P,Q, dan R adalah titik-titik sembaang dalam sistem koordinat cartesius maka vektor OP,OQ dan QR dapat diwakili oleh vektor-vektor p,q dan r. vektor-vektor p,q, dan r disebut vektor posisi dari titik-titik P,Q dan R.
1. PERBANDINGAN SEGMEN GARIS
Perbandingan segmen garis pada gambar 5.38 (a) dinamakan perbandingan di dalam,sedangkan perbandingan segmen garis pada gambar 5.38 (b) dan gambar 5.38 (c) adalah perbandingan diluar.
sekarang,perhatikan gambar berikut.
Pada gambar diatas,diketahui vektor posisi titik P dan Q berturut-turut adalah vektor p dan q.titik R pada ruas garis PQ mempunyai perbandingan m : n atau PR : RQ = m : n. jika vektor posisi titik R adalah r, untuk menentukan vektor r dapat dilakukan dengan cara berikut:
PR : RQ = m : n
= nPR = mRQ
= n (r - p)= m (q - r)
= n r + mr = mq + np
= r= mq + np/ m+n
jadi,berdasarkan gambar diatas vektor r dapat dinyatakan dengan rumus
Rumus ini dapat digunakan untuk vektor yang berada dalam ruang (dimensi tiga).
2. TITIK-TITIK SEGARIS (KOLINEAR)
Tentu kalian masih ingat bahwa jika k suatu skalar dan a = kb maka a dan b sejajar . Demikian juga , jika AB = kBC maka AB dan BC sejajar.
perhatikan gambar berikut:
Titik-titik P , Q dan R terletak segaris.Pasti PQ sejajar dengan QR sehingga dapat ditulis PQ = kQR. (ingat syarat dua garis sejajar). karena Q adalah titik yang sama-sama dilalui oleh PQ dan QR maka P,Q dan R adalah segaris jadi, dua atau tiga garis dikatakan segaris, selain garis-garis itu sejajar, juga harus mempunyai titik yang sama-sama dilalui garis-garis itu
Titik P,Q dan R segaris jika dapat dituliskan PQ=kQR dan Q titik yang sama-sama dilalui oleh PQ dan QR
3. TEOREMA CEVA(PENGAYAAN)
Perhatikan gamabar di bawah ini
Misalkan diberikan segitiga ABC. Titik D,E dan F berturut-turut terletak pada sisi CA,AB dan BC sedemikian rupa sehingga ruas garis AF,BD dan CE berpotongan disatu titik maka berlaku teorema ceva berikut.
E. PROYEKSI ORTOGONAL SUATU VEKTOR PADA VEKTOR LAIN
Tahukah kalian apakah arti proyeksi? Kali ini kita akan mempelajari proyeksi ortogonal suatu vektor pada vektor lain. Sebelum mempelajarinya lebih lanjut,
Pada gambar tersebut, proyeksi titik A pada ruas garis AD adalah titik A sendiri. Proyeksi titik B pada ruas garis AD adalah titik C. Bagaimana dengan proyeksi ruas garis AD? Tentu, proyeksi ruas garis AB pada ruas garis AD adalah ruas garis AC.
Vektor c adalah proyeksi ortogonal a pada vektor b. Vektor c dapat diperoleh dengan menarik titik ujung vektor a, kemudian memproyeksikannya pada vektor b. Vektor c ini memiliki arah yang sama dengan arah vektor b. Vektor c dapat ditentukan dengan cara berikut.
Bagaimana menentukan panjang proyeksi ortogonal vektor a pada vektor b? Kita telah menemukan vektor c yang merupakan vektor proyeksi ortogonal vektor a pada vektor b. Kita akan menemukan panjang proyeksi ortogonal vektor a pada vektor b,yaitu |c|. Perhatikan ilustrasi pada gambar berikut :
Pada gambar diketahui panjang vektor a adalah |a| dan panjng vektor c adalah |c|. Pada Gambar 5.51,kita dapat memperoleh:
Nilai |c| inilah yang merupakan panjang proyeksi ortogonal vektor a pada vektor b . Perlu juga kalian ketahui bahwa panjang proyeksi ortogonal vektor a pada vektor b biasanya disebut sebagai proyeksi skalar ortogonal dari vektor a pada vektor b.



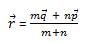







Tidak ada komentar:
Posting Komentar