DEFINISI VEKTOR

Hai Kami dari dailyvector_mat!!! Seperti namanya,kami adalah salah satu kelompok belajar yang akan membahas materi tentang vektor dan kami berharap apa yang kami jelaskan dapat bermanfaat bagi teman-teman yang membaca blog kami. Ayo teman-teman dibaca dengan seksama yahhhh !!!!!

Nama anggota kelompok:

Rahmah Aulia Putri

Andi Tantri

Septiana Dian

Imel Van Asti

Keisha Nikol

Lady Meirizki

Meli Handayani

Prima Jenny

Agung Ramadhan

Muh.Arfan

Muh.Rizki

Muh.Irsan 

                                                                                         

A. Definisi vektor dan operasinya

1. Definisi vektor                                 

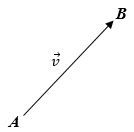
      Vektor adalah besaran yang mempunyai  nilai dan arah. nilai disini maksudnya panjang dari vektor tersebut sedangkan arahnya sesuai dengan mata angin.suatu vektor dinamai dengan huruf kecil dengan tanda panah diatasnya maupun dibawahnya. Vektor juga sering dinotasikan dengan huruf kecil cetak tebak misalnya v. Perhatikan gambar di samping. Pada gambar disamping vektor v yang mempunyai titik pangkal dititik A dan titik ujung dititik B. sehingga, panjang vektor v adalah panjang dari titik A ke titik B.  Dalam bentuk matriks vektor v dapat dituliskan sebagai berikut:

       Untuk komponen x, jika arahnya kekananmaka tandanya positif,sedangkan jika arahnya ke kiri,maka tandanya negatif. Untuk komponen y jika arahnya ke atas, berarti tandanya positif, sedangkan arahnya ke bawah tandanya negatif.

      Selain nilai dan arah ada beberapa hal yang berhubungan dengan vektor yaitu jarak dan perpindahan. Misalnya Rahmah dan Tantri berjarak 4 m, kemudian Rahmah berjalan ke arah Tantri maka jarak dan perpindahannya adalah 4 m. Namun jika Rahmah kembali ke tempat awal ia berdiri maka jaraknya akan berubah menjadi 8 m sedangkan perpindahannya menjadi 0.

2. Operasi aljabar pada vektor

      Sebagaimana bilangan pada vektor juga berlaku operasi aljabar atau lebih dikenal dengan kalibataku yaitu kali,bagi,tambah,dan kurang. Dalam penjumlahan dan pengurangan vektor berlaku 2 cara yaitu cara segitiga dan cara jajargenjang. 

a. Penjumlahan vektor

        

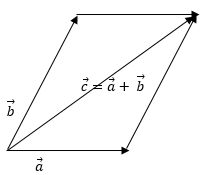
Pada gambar di atas terdapat dua buah vektor pada bidang cartesius yaitu vektor a dan b. Dapat kita lihat bahwa 

Cara segitiga :

Contoh

Perhatikan gambar di bawah ini!

Gambarlah vektor AB +  BC dan tentukan komponen x dan komponen y vektor AC

Jawab : 

Cara jajargenjang:

        Secara geometris, resultan hasil penjumlahan vektor a dan b yaitu c = a + b   dapat digambarkan seperti gambar di samping. Terlebih dahulu,geser vektor b sehingga titik pangkal b berimpit pada titik pangkal a. Dalam hal ini, vektor b tidak berubah besar dan arahnya. Selanjutnya buatlah jajargenjang semu yang di bentuk oleh vektor a dan b. Vektor c adalah vektor yang berimpit dengan diagonal utama jajargenjang tersebut.

b. Pengurangan vektor

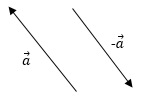
      Pengurangan vektor tidak jauh berbeda dari penjumlahan vektor. namun dalam pengurangan vektor jika sebuah vektor a mempunyai arah timur laut, maka vektor -a mempunyai arah yang berlawanan yaitu barat daya.Perhatikan gambar di bawah ini!

Seperti yang kalian ketahui jika arah suatu vektor berlawanan dengan arah vektor semula misalnya vektor a dapat dituliskan vektor -a.

c. Perkalian vektor dengan skalar

                                    

Berdasarkan gambar di atas, dalam bentuk vektor kolom vektor a dapat ditulis sebagai berikut.

Berdasarkan sifat perkalian matriks dengan skalar maka 

                   

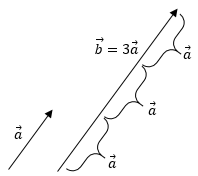
Misalkan vektor b adalah vektor yang searah dengan vektor a,tetapi memiliki panjang 3 kali vektor a.Vektor b dapat di tuliskan dengan b = 3a .Apabila vektor b memiliki arah yang berlawanan maka b dapat dituliskan dengan b = -3a.

Contoh soal 

          




Jawab 

Agar lebih jelas dan lebih mudah dipahami, materi ini dapat didownload dalam format PDF dengan mengklik link di bawah ini!
Download PDF

Terima kasih bagi teman-teman yang sudah membaca blog kami dan kami meminta maaf apabila ada kata maupun kalimat yang kurang baik . THANK YOU FOR READ IT 💓💓💓